Desigualdades Lineales

Walter Mora Flores

Un experimento con LaTeX, html, make4ht, MathJax, DeepSeek y chatGPT

Contenido
Intervalos
Intersección de intervalos
Unión de intervalos

1. Intervalos

Imaginemos que vamos a comprar tela y que el metro vale $\colon \, 1000$ el metro. Si solo tenemos $\p{\colon 20\\,000}$, entonces como máximo, podremos comprar $\p{20}$ metros de tela.
Si denotamos con "$x$" la cantidad de metros de tela que vamos a comprar, entonces la situación de comprar "$x$" metros de tela se puede describir como "$0\leq \;\mbox{metros de tela}\; \leq 20$".

Usando la notación de conjuntos escribimos: $\p{\{x \tq 0\leq x\leq 20\}}$ y podemos hacer una representación gráfica de este conjunto en la recta real.

Figura 1.1: "

x

" metros de tela en un intervalo de

0

20

Pero en la realidad pasan situaciones como "voy a comprar entre $5$ metros y $10$ metros" o "voy a comprar más de $5$ metros pero estrictamente menos de $20$ metros". Estas situaciones las podemos escribir así:

Situación en palabras: Comprar " $x$ " metros de tela en un intervalo		Descripción del intervalo

"voy a comprar entre $5$ metros y $10$ metros"		$5 \leq x \leq 10$

"voy a comprar $5$ o más metros pero menos de $20$ metros"		$5 \leq x < 20$

"voy a comprar más de $5$ metros pero menos de $10$ metros"		$5 < x < 10$

Notación de intervalos y representación gráfica

También usamos una notación con paréntesis cuadrados para describir un intervalo.

$∙$

El intervalo es "cerrado" en un extremo si el extremo se incluye y es "abierto" en un extremo si ese extremo se excluye.

$∙$

Un intervalo es cerrado si ambos extremos se incluyen y lo denotamos como

[a, b]

$∙$

Un intervalo es abierto si ambos extremos se excluyen y lo denotamos como

] a, b [

$∙$

Un intervalo es semiabierto si algún extremo se excluye, por ejmplo

] a, b]

[a, b [

$∙$

Para realizar la representación gráfica de un intervalo procedemos así:

$∙$: Dibujamos un segmento de recta de longitud adecuada
$∙$: Dibujamos un segmento más grueso que inicia y finaliza en en los extremos del intervalo
$∙$: En los extremos del segmento, dibujamos un disco relleno si el extremo está incluido en el intervalo y un disco sin relleno si el extremo no está incluido.

En estos intevalos suponemos que $a \leq b$

Notación en términos de desigualdades	Notación de intervalo con paréntesis cuadrados	Representación gráfica

$a \leq x \leq b$	$[a, b]$

$a < x \leq b$	$] a, b]$

$a < x < b$	$] a, b [$

$a \leq x < b$	$[a, b [$

En el script que sigue puedes:

Arrastrar con el ratón sobre los extremos. Los extremos del intervalo cambian
Hacer doble click sobre algún extremo del intervalo. Cambia su estado, es decir, si esta cerrado pasa a abierto y si esta abierto pasa a cerrado.
Se actualiza el intervalo con notación de paréntesis cuadrados

Script interactivo. En los extremos del intervalo: arrastre o haga doble click.

Casos especiales: Como $a \leq b$ podemos tener el caso $a = b .$ En esta situación:

1.: $[a, a] = a$
2.: $[a, a [= \emptyset,] a, a] = \emptyset,] a, a [= \emptyset$
3.: A veces en un intervalo se excluye un valor, por ejemplo $[2, 6 [- 3$ indica que que en el intervalo $[$ 2,6[ además del extremo " $6$ ", también se excluye el valor " $3$ "

Ejemplo

En la siguiente tabla se muestran seis filas. En cada fila, las columnas describen un intervalo de las maneras distintas que hemos indicado.

En la primera columna: Notación en términos de desigualdades. En la segunda columna: Notación de intervalo con paréntesis cuadrados y en la tercera columna: Representación gráfica

$- 1 \leq x \leq 3$		$[- 2, 3]$

$5 < x \leq 7$		$] 5, 7]$

$4 \leq x \leq 4$		$[4, 4]$

$2 \leq x < 4$		$[2, 4 [$

$2 \leq x \leq 3$		$[2, 3]$

$1 \leq x < 7$		$[1, 7 [$

Ejercicios

En el "script" (programa) que sigue, puede presionar el botón "Generar Intervalo" para generar un intervalo. Luego en papel, dibuje la representación gráfica del intervalo. Presione el botón "Dibujar intervalo" para verificar su respuesta.

Script: Generar intervalo y realizar representación gráfica

Intervalo

1.2 Intersección de intervalos

Dos intervalos pueden tener elementos en común. La intersección de dos intervalos es el conjunto de elementos que tienen estos intervalos en común. Si no tienen elementos en común, la intersección el el conjunto vacío ( $\emptyset$ )

Determinando la intersección de dos intervalos

$∙$: Dibujamos una recta numérica
$∙$: Dibujamos cada intervalo sobre la recta con un segmeto grueso o con colores distintos, icluyendo los discos para sus extremos
$∙$: La intersección es el segmento que tienen en común ambos intervalos. Si algún intervalo tiene un (o dos) extremo abierto, este valo no puede estar en la intersección por no ser un valor que esta en los dos intervalos.

Ejemplo

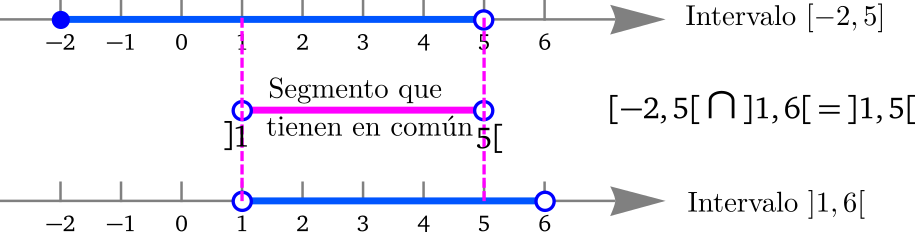
Realizar la representación gráfica y calcular la intersección de los intervalos $[- 2, 5 [$ y $] 1, 6 [,$ es decir, calcular $[- 2, 5 [\cap] 1, 6 [$ y hacer la representación gráfica.

Solución: Podemos dibujar cada intervalo por separado y luego marcar el segmento de intersección. En este caso se ve que lo que tiene en común va de $1$ hasta $5$ pero no podemos tomar el $1$ ni el $5$ porque no son elementos de ambos intervalos.

Figura 1.2: Intersección de los intervalos

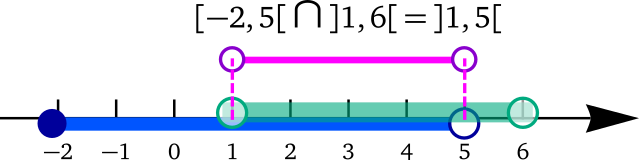
Otra manera es dibujar ambos intervalos en una misma recta y resaltar el segmento de intersección.

Figura 1.3: Intersección de los intervalos

Ejemplo

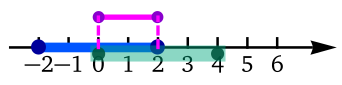
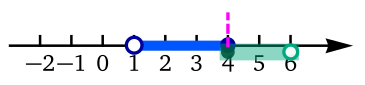
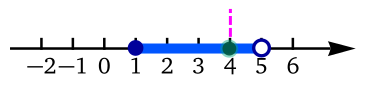
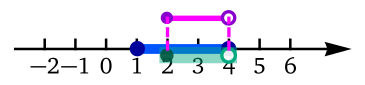
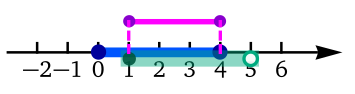
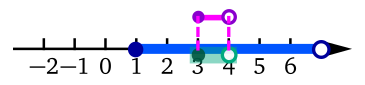
En la siguiente tabla se muestran seis filas. En cada fila, la primera columna indica la intersección usando notación con paraéntesis cuadrados y la segunda columna la representación gráfica de la intersección.


$[- 2, 2] \cap [0, 4] = [0, 2]$

$] 1, 4] \cap [4, 6 [= {4}$

$[4, 4] \cap [1, 5 [= {4}$

$[2, 4 [\cap [1, 4] = [2, 4 [$

$[0, 4] \cap [1, 5 [= [1, 4 [$

$[1, 7 [\cap [3, 4 [= [3, 4 [$

En el script que sigue puedes:

Arrastrar con el ratón sobre los extremos: Los extremos del intervalo cambian
Hacer doble click sobre algún extremo del intervalo: Cambia su estado, es decir, si esta cerrado pasa a abierto y si esta abierto pasa a cerrado.
Se actuliza el intervalo con notación de paréntesis cuadrados y se calcula la intersección

Script: En los extremos de los intevalos: Arrastre o haga doble click

Ejercicios

En el "script" (programa) que sigue, puede:

Presionar el botón "Generar Intervalos" para generar un par de intervalos y su representación gráfica.
Luego en papel,calcule la intersección y dibuje la representación gráfica de la intersección de los intervalos.
Presione el botón "Cálculo y representación gráfica" para verificar su respuesta.

Script interactivo: Con los botones genere un intervalo y realice la representación gráfica.

$ \cap $

1.3 Unión de intervalos

La unión de dos intervalos es el conjunto de elementos que están en ambos intervalos

Determinando la unión de dos intervalos

$∙$: Dibujamos una recta numérica
$∙$: Dibujamos cada intervalo sobre la recta con un segmeto grueso o con colores distintos, icluyendo los discos para sus extremos
$∙$: La unión es el segmento (o los segmentos) que representan los intervalos. La parte donde se traslapan (si hubiera) solo se considera una vez.

Ejemplo

Realizar la representación gráfica y calcular la unión de los intervalos $[- 2, 5 [$ y $] 1, 6 [,$ es decir, calcularr $[- 2, 5 [\cup] 1, 6 [$ y hacer la representación gráfica.

Solución: Podemos dibujar cada intervalo por separado y luego marcar el segmento (o segmentos) que representan la unión. En este caso se ve que la unión va de $- 2$ hasta $6$ pero sin incluir el $6 .$ El traslape de ambos intervalos solo se toma en cuenta una vez. De esta manera podemos concluir que

[- 2, 5 [\cup] 1, 6 [= [- 2, 6 [

Figura 1.4: Uniónde los intervalos

Ejemplo

En la siguiente tabla se muestran seis filas. En cada fila, la primera columna indica la unión usando notación con paraéntesis cuadrados y la segunda columna la representación gráfica de esta unión.

$[- 2, 2] \cap [0, 4] = [- 2, 4]$

$] 1, 4 [\cap [4, 6 [=] 1, 6 [$

$[4, 4] \cap [1, 5 [= [1, 5 [$

$[2, 4 [\cap [1, 4] = [2, 4]$

$[0, 4] \cap] 1, 5 [= [0, 5 [$

$[- 2, 0 [\cap [1, 3 [= [- 2, 0 [\cap [1, 3 [$

$[- 2, 1 [\cap] 1, 3 [= [- 2, 3 [- {1}$

En el script que sigue puedes:

Arrastrar con el ratón sobre los extremos. Los extremos del intervalo cambian
Hacer doble click sobre algún extremo del intervalo. Cambia su estado, es decir, si esta cerrado pasa a abierto y si esta abierto pasa a cerrado.
Calcula la unión de estos intervalos con paréntesis cuadrados

Script interactivo: Con los extremos: Arrastre y/o haga doble click

Ejercicios

En el "script" (programa) que sigue, puede:

Presionar el botón "Generar Intervalos" para generar un par de intervalos.
Luego en papel,calcule la unión de estos intervalos y dibuje la representación gráfica de la unión de los intervalos.
Presione el botón "Cálculo y representación gráfica" para verificar su respuesta.

Script interactivo: Con los botones genere un intervalo y realice la representación gráfica de la unión.

$ \cup $